Breakthrough Proof Clears Path For Quantum AI
Eddie Gonzales Jr. – MessageToEagle.com – Convolutional neural networks running on quantum computers have generated significant buzz for their potential to analyze quantum data better than classical computers can. While a fundamental solvability problem known as “barren plateaus” has limited the application of these neural networks for large data sets, new research overcomes that Achilles heel with rigorous proof that guarantees scalability.
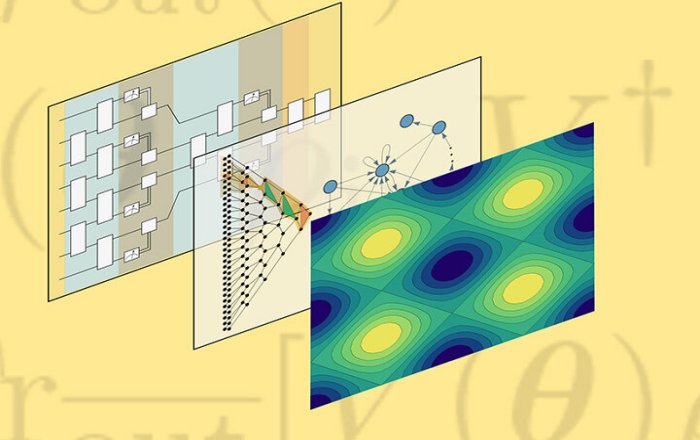
A novel proof that certain quantum convolutional networks can be guaranteed to be trained clears the way for quantum artificial intelligence to aid in materials discovery and many other applications. Credit: Los Alamos National Laboratory
“The way you construct a quantum neural network can lead to a barren plateau—or not,” said Marco Cerezo, co-author of the paper titled “Absence of Barren Plateaus in Quantum Convolutional Neural Networks,” published today by a Los Alamos National Laboratory team in Physical Review X. Cerezo is a physicist specializing in quantum computing, quantum machine learning, and quantum information at Los Alamos.
“We proved the absence of barren plateaus for a special type of quantum neural network. Our work provides trainability guarantees for this architecture, meaning that one can generically train its parameters.”
As an artificial intelligence (AI) methodology, quantum convolutional neural networks are inspired by the visual cortex. As such, they involve a series of convolutional layers, or filters, interleaved with pooling layers that reduce the dimension of the data while keeping important features of a data set.
These neural networks can be used to solve a range of problems, from image recognition to materials discovery. Overcoming barren plateaus is key to extracting the full potential of quantum computers in AI applications and demonstrating their superiority over classical computers.
Until now, Cerezo said, researchers in quantum machine learning analyzed how to mitigate the effects of barren plateaus, but they lacked a theoretical basis for avoiding it altogether. The Los Alamos work shows how some quantum neural networks are, in fact, immune to barren plateaus.
“With this guarantee in hand, researchers will now be able to sift through quantum-computer data about quantum systems and use that information for studying material properties or discovering new materials, among other applications,” said Patrick Coles, a quantum physicist at Los Alamos and a coauthor of the paper.
Many more applications for quantum AI algorithms will emerge, Coles thinks, as researchers use near-term quantum computers more frequently and generate more and more data—all machine learning programs are data-hungry.
Avoiding the vanishing gradient
“All hope of quantum speedup or advantage is lost if you have a barren plateau,” Cerezo said.
The crux of the problem is a “vanishing gradient” in the optimization landscape. The landscape is composed of hills and valleys, and the goal is to train the model’s parameters to find the solution by exploring the geography of the landscape. The solution usually lies at the bottom of the lowest valley, so to speak. But in a flat landscape one cannot train the parameters because it’s difficult to determine which direction to take.
That problem becomes particularly relevant when the number of data features increases. In fact, the landscape becomes exponentially flat with the feature size. Hence, in the presence of a barren plateau, the quantum neural network cannot be scaled up.
The Los Alamos team developed a novel graphical approach for analyzing the scaling within a quantum neural network and proving its trainability.
For more than 40 years, physicists have thought quantum computers would prove useful in simulating and understanding quantum systems of particles, which choke conventional classical computers. The type of quantum convolutional neural network that the Los Alamos research has proved robust is expected to have useful applications in analyzing data from quantum simulations.
“The field of quantum machine learning is still young,” Coles said. “There’s a famous quote about lasers, when they were first discovered, that said they were a solution in search of a problem. Now lasers are used everywhere. Similarly, a number of us suspect that quantum data will become highly available, and then quantum machine learning will take off.”
For instance, research is focusing on ceramic materials as high-temperature superconductors, Coles said, which could improve frictionless transportation, such as magnetic levitation trains. But analyzing data about the material’s large number of phases, which are influenced by temperature, pressure, and impurities in these materials, and classifying the phases is a huge task that goes beyond the capabilities of classical computers.
Using a scalable quantum neural network, a quantum computer could sift through a vast data set about the various states of a given material and correlate those states with phases to identify the optimal state for high-temperature superconducting.
Written by Eddie Gonzales Jr. MessageToEagle.com Staff